Как научиться делить столбиком (уголком): примеры с решениями и объяснением

Правила деления в столбик

Без остатка

Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.

Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:

1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.

2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.

Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.

3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица

Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления

Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.

4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.

Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.

5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.

На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.

С остатком

В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.

Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).

Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.

Обучение делению с остатком

Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:

• Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
• Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
• Запишите под числом 35 число 32.
• Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.

Деление с остатком

Простые примеры для ребенка

На этом же примере можно продолжить:

• При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
• При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
• Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
• В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
• При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.

Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.

Как научиться делить столбиком на двузначное

В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.
Конечно, такое деление сложнее однозначного, но при правильном подходе и понимании оно не составит труда. Здесь важен правильный подбор чисел и постепенное освоение темы, от простого к сложному.

Для примера выполним действие: 144 : 24

Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т.е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.

Разделим 1035 на 23.

Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11. Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.

Как правильно подготовить ребенка к восприятию нового материала?

Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.

Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.

Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

3. Выполняем операцию вычитания  и под чертой записываем результат.

4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

Ответ: 1006005

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

В частном будет однозначное число. 

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

 Значение частного чисел 768 и 24 равно 32.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое  414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

на доске решены примеры на деление столбиком трёх- и более значных чисел

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

алгоритм деления столбиком четырёхзначного числа

пример деления столбиком четырёхзначного числа на двузначное

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

примеры деления столбиком многочленов

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

примеры деления многочленов в столбик

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.
2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Как делить в столбик с остатком?

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

1. Расскажите ученику третьего класса, что не все цифры можно поделить поровну. Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
2. Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).

Деление с остатком

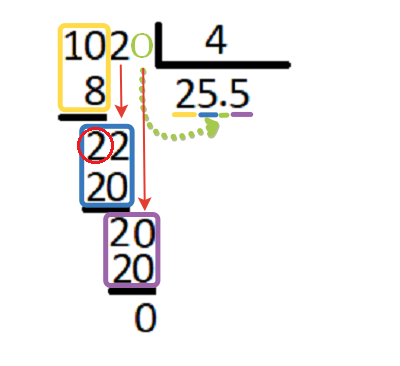
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

слайд из презентации о делении чисел с остатком

Запишите его в ответе либо:

• как дробь, где в числителе остаток, а в знаменателе — делитель
• словами, например, 73 целых и 6 в остатке

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Пример деления

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

• Напишите в тетради пример: 105 разделить на 5.
• Запишите это, как при делении в столбик.
• Расскажите, что 105 – делимое, а 5 – делитель.
• С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
• В столбике деления, под числом 5, напишите цифру 2.
• Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
• Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
• В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.

Еще один пример деления

Как пошагово объяснить алгоритм математического действия?

Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:

Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части

Важно указать ребенку, что ответ не должен превышать 9.
Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
Далее, нужно найти разницу между частью делимого и полученным произведением.
Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.

Проверочные работы по математике на тему “Умножение и деление многозначных чисел”(4 класс)

Самостоятельная работа по теме: «Умножение и деление на двузначное число»

4 класс, 3 четверть

вариант I

1. Решите пример на деление:

336 : 3 = 138 : 46 =

750 : 50 = 640 : 80 =

1. Решите пример на умножение:

132 * 59 = 631 * 60 =

72 * 20 = 86 * 26 =

1. Решите задачу:

На склад поступило 2 тонны 640 кг муки. Затем 13 мешков по 48 кг в каждом отдали в производство. Сколько муки осталось на складе?

1. Решите задачу:

Из точки А и точки В на встречу друг другу одновременно выехали 2 велосипедиста. Расстояние между точками равно 200 км. Они встретились через 5 часов. С какой скоростью двигался первый велосипедист, если скорость второго была равна 18 км/час?

1. Найдите значение выражений:

32 568 – (2 832 * 7 + 3 202 : 2) = (1652 * 7 – 237 : 3) – 238 =

вариант II

1. Решите пример на деление:

350 : 50 = 230 : 46 =

483 : 3 = 320 : 80 =

2. Решите пример на умножение:

47 * 30 = 312 * 61 =

245 * 30 = 48 * 27 =

3. Решите задачу:

На склад в магазин привезли 2830 кг сахара. Каждый день продавали по 68 кг. Сколько сахара осталось на складе после 23 дней?

4. Решите задачу:

Из двух населенных пунктов на встречу друг другу вышли 2 путника. Расстояние между населенными пунктами равно 84 км. Они встретились через 6 часов. С какой скоростью шел первый путник, если скорость второго была равна 8 км/час?

5. Найдите значение выражений:

18 345 – (5 358 * 2 + 3 208 : 2 ) = (6 785 * 3 – 8 120 : 4) – 2 458 =

вариант III

1. Решите пример на деление:

276 : 46 = 840 : 40 =

453 : 3 = 990 : 30 =

2. Решите пример на умножение:

186 * 35 = 23 * 80 =

43 * 50 = 134 * 70 =

3. Решите задачу:

В цех привезли 3 654 заготовки. В токарный цех каждый день направляют по 37 деталей. Сколько деталей осталось в цеху через 40 дней?

4. Решите задачу:

Из двух городов на встречу друг другу выехали 2 мотоциклиста. Расстояние между городами равно 840 км. Они встретились через 7 часов. С какой скоростью ехал первый мотоциклист, если скорость второго была равна 70 км/час?

5. Найдите значение выражений:

29 235 – (3 984 * 6 + 6 788 : 2 ) = (8 102 – 246 : 3) – 315 * 4 =

Самостоятельная работа по теме: «Умножение и деление на трёхзначное число»

4 класс, 4 четверть

вариант I

1. Выполните деление:

31 901 : 73 = 33 387 : 93 =

309 888 : 384 = 127 270 : 143 =

2. Выполните умножение:

213 * 307 = 836 * 167 =

589 * 372 = 430 * 132 =

3. Переведите:

5 часов 13 минут = … сек 1 тонн 3 центнеров 68 кг = … кг

1 км 43 метра = … дм 28 часов 42 мин = … мин

4. Решите задачу:

Отряд пионеров прошел 20 км. Это составляет четверть пути. Сколько должны пройти пионеры?

вариант II

1. Выполните деление:

25 296 : 68 = 6 279 : 13 =

111 948 : 114 = 173 990 : 274 =

2. Выполните умножение:

248 * 357 = 721 * 163 =

701 * 591 = 231 * 694 =

3. Переведите:

1 час 48 минут = … сек 4 тонн 8 центнеров 213 кг = … кг

2 км 483 метров = … дм 1 сутки 8 часов = … мин

4. Решите задачу:

Спортсмены пробежали 15 км. Это составляет треть пути. Сколько должны пробежать спортсмены?

вариант III

1. Выполните деление:

218 654 : 218 = 716 982 : 794 =

99 264 : 132 = 54 544 : 487 =

2. Выполните умножение:

478 * 306 = 404 * 715 =

213 * 372 = 397 * 702 =

3. Переведите:

3 часа 38 минут = … сек 13 тонн 7 центнеров 63 кг = … кг

16 км = … дм 4 часов 37 мин = … мин

4. Решите задачу:

Велосипедисты проехали 18 км. Это составляет пятую часть пути. Сколько должны проехать велосипедисты?

Самостоятельная работа по теме: « Итоговое повторение»

4 класс, 4 четверть

вариант I

1. Решите пример:

3 758 + 6 345 = 27 397 – 7 164 =

782 * 23 = 33 948 : 82 =

2. Найдите значения выражений:

3 000 : 60 – 250 : 50 =

( 213 173 – 19 403 ) : 2 – 31 * 73 =

3. Решите задачу:

Из пункта А одновременно в одном направлении выехали мотоциклист и велосипедист. Скорость мотоциклиста 72 км/час, а велосипедиста 25 км/час. Какое расстояние будет между ними через 3 часа?

вариант II

1. Решите пример:

7 165 + 18 448 = 55 103 – 731 =

694 * 36 = 18 144 : 567 =

2. Найдите значения выражений:

5 600 : 70 + 210 : 70 =

( 14 864 – 3 486 ) : 2 – 19 * 26 =

3. Решите задачу:

Из двух населенных пунктов одновременно навстречу друг другу выехали поезд и автомобиль. Скорость поезда 48 км/час, а автомобиля 72 км/час. Через какое время они встретятся, если расстояние между городами 360 км?

вариант III

1. Решите пример:

4 138 + 12 672 = 63 230 – 879 =

736 * 34 = 35 805 : 35 =

2. Найдите значения выражений:

4 200 : 60 – 490 : 70 =

( 114 378 – 21 366 ) : 2 – 31 * 72 =

3. Решите задачу:

Из одного города одновременно в разных направлениях выехали мотоциклист и велосипедист. Скорость автомобиля 65 км/час, а велосипедиста 25 км/час. Какое расстояние будет между ними через 3 часа?

Обучение делению с остатком

Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:

• Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
• Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
• Запишите под числом 35 число 32.
• Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.

Простые примеры для ребенка

На этом же примере можно продолжить:

• При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
• При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
• Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
• В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
• При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.

Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.