Как быстро научить ребенка делить столбиком?

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Решим пример \(\textcolor{red} {295383\div 34}\).

Далее записываем известные
компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру
разряда тысяч, а под неполным делимым пишем результат произведения неполного
частного и делителя. И сразу же находим остаток от этого действия, т.е.
вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor{red} {8\cdot 37=272}\). Записываем его под 295 и находим разницу: \(\textcolor{red} {295-272=23}\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

Находим результат деления второго неполного делимого на делитель. 233 сотни разделить на 34 будет 6 сотен. Значит, в разряде сотен частного будет цифра 6. Умножаем ее на делитель 34, получаем 204 и еще 29 сотен неразделенных.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

При делении второго неполного делимого 298 десятков на делитель 34 получается 8 десятков, и еще 26 десятков неразделенных (как и в предыдущих действиях, я умножил 8 на 34 и результат отнял от 298). Поэтому, в частном, в разряде десятков записываем цифру 8.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Разделив 263 единицы на 34, получаем 7 полных единиц и 25 неразделенных. Записав в частном последнюю цифру разряда единиц, получаем окончательный ответ действия \(\textcolor{red} {295383\div 34=8687}\) и 25 в остатке.

Рассмотрим еще один пример. \(\textcolor{red} {25326\div 63}\).

Первое неполное делимое будет 253 сотни, количество цифр в частном – 3.

Делим 253 сотни на 63, получается 4 полных сотни и неразделенная 1 сотня в остатке.

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Но 12 не делится нацело на 63 части, то есть, нет ни одного целого десятка в каждой части. Значит, мы в частном в разряде десятков должны записать , поскольку все 12 десятков оказались неразделенными. А к этим 12 десяткам (т.е. 120 сотням) добавить (снести) 6 единиц делимого.

Итак, запомните, что
каждое неполное делимое образует в частном одну цифру соответствующего разряда
и что даже если неполное делимое меньше делителя, то в частном все равно нужно
записать нулевой результат этого действия.

126 единиц делим на 63, получается 2 единицы без остатка. Теперь мы можем записать окончательный ответ деления \(\textcolor{red} {25326\div 63=402}\).

Итак, в общем виде алгоритм деления в столбик выглядит так:1. Находим первое неполное делимое и количество цифр в частном.2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.4. Ставим между ними знак минус и выполняем действие.5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.7. Если неполное делимое невозможно разделить на делитель, то в частном ставится и к этому неполному делимому сносится следующая цифра.

Как делить столбиком

Допустим, нам нужно разделить  780  на  12,  записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число  7,  так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число  78  больше делителя, поэтому мы начинаем деление с него:

В нашем случае число  78  будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра —  0,  это значит, что частное будет состоять из  2  цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз  12  содержится в числе  78.  Для этого мы последовательно умножаем делитель на натуральные числа  1, 2, 3, …,  пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число  6,  записываем его под делитель, а из  78  (по правилам вычитания столбиком) вычитаем  72  (12 · 6 = 72).  После того, как мы вычли  72  из  78,  получился остаток  6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше

К получившемуся остатку —  6,  сносим следующую цифру делимого —  0.  В результате, получилось неполное делимое —  60.  Определяем, сколько раз  12  содержится в числе  60.  Получаем число  5,  записываем его в частное после цифры  6,  а из  60  вычитаем  60  (12 · 5 = 60).  В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит  780  разделилось на  12  нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

780 : 12 = 65.

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить  9027  на  9.

Определяем неполное делимое — это число  9.  Записываем в частное  1  и из  9  вычитаем  9.  В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого —  0.  Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль  (0 : 9 = 0)  и в промежуточных вычислениях из  0  вычитаем  0.  Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого —  2.  В промежуточных вычислениях вышло так, что неполное делимое  (2)  меньше, чем делитель  (9).  В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз  9  содержится в числе  27.  Получаем число  3,  записываем его в частное, а из  27  вычитаем  27.  В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число  9027  разделилось на  9  нацело:

9027 : 9 = 1003.

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить  3000  на  6.

Определяем неполное делимое — это число  30.  Записываем в частное  5  и из  30  вычитаем  30.  В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого —  0.  Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из  0  вычитаем  0:

Сносим следующую цифру делимого —  0.  Записываем в частное ещё один нуль и в промежуточных вычислениях из  0  вычитаем  0.  Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток —  0.  Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит  3000  разделилось на  6  нацело:

3000 : 6 = 500.

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, с нулями, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем и правил в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

Понравился наш контент? Подпишитесь на канал в .

Обучение делению в столбик в форме игры

Можно поставить задачи таким образом:

1Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.

2Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.

3Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.

4Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.

Деление чисел

Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.

Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.

Как научиться делить столбиком на двузначное

В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.
Конечно, такое деление сложнее однозначного, но при правильном подходе и понимании оно не составит труда. Здесь важен правильный подбор чисел и постепенное освоение темы, от простого к сложному.

Для примера выполним действие: 144 : 24

Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т.е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.

Разделим 1035 на 23.

Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11. Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.

Обучение делению чисел столбиком с нолями

Деление чисел с нолями идентично обычному делению. Родителям нужно объяснить ребенку основные нюансы:

• Расскажите, что если в конце делимого и делителя есть ноли, то их можно зачеркивать в уме. Предложите школьнику зачеркивать их простым карандашом для понимания. Дальше нужно делить, как и в обычных примерах. Например, если 1200 нужно разделить на 400, то ребенок может сократить пример, убрав два 0 у обоих чисел. А в примере деления 15600 на 560 можно сократить только по одному 0.
• Объясните ученику, что если 0 есть только в делителе, то его нельзя сокращать.

Чтобы лучше усваивать материал, можно решить простой пример деления:

• Запишите в тетради пример: 100 разделить на 10. Это легкий пример, так как при сокращении нолей он представлен так: 10 разделить на 1.
• Ребенку следует под делителем написать цифру 10. Так как при умножении 1 на 10 получается требуемый результат. Под делимым ребенку нужно записать 10. Остатка у этого примера нет.

Предложите ребенку легкие примеры такого типа:

• 200 разделить на 20;
• 300 разделить на 30;
• 400 разделить на 40;
• 500 разделить на 50;
• 600 разделить на 60;
• 700 разделить на 70.

Далее можно переходить к сложным примерам. Но только после того, как ребенок усвоит результат.

Как делить в столбик с остатком?

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

1. Расскажите ученику третьего класса, что не все цифры можно поделить поровну. Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
2. Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).

Деление с остатком

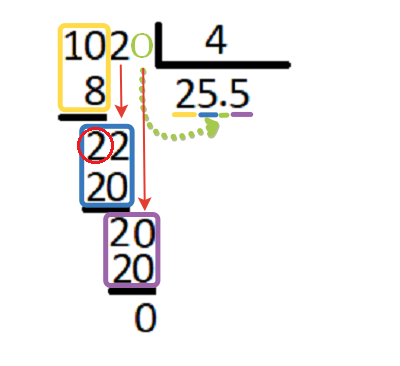
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

слайд из презентации о делении чисел с остатком

Запишите его в ответе либо:

• как дробь, где в числителе остаток, а в знаменателе — делитель
• словами, например, 73 целых и 6 в остатке

Решение задач с единицами площади

Ребята, взрослые люди часто испытывают досаду, занимаясь ремонтом дома или квартиры. Почему? Знакома ситуация, когда чуть-чуть не хватило краски или обоев? Нужно срочно бежать в магазин, чтобы купить недостающие материалы. Можно ли этого избежать? Конечно, можно! Главное, правильно выполнить расчеты. Например, правильно измерить площадь пола под покраску или площадь стен под обои.

Задача

В комнате длиной 7 м и шириной 8 м укладывают на пол ламинат квадратами 50х50 см. Сколько штук ламината потребуется для этой комнаты?

Подсказка. Вычислите площадь комнаты и площадь одного квадрата ламината. Одинаковые ли единицы площади вы использовали? Выразите квадратные метры в квадратных сантиметрах.

Решите задачу самостоятельно.

Проверь себя.

S пола = 7 ∙ 8 = 56 (м²)

S лам. = 50 ∙50 = 2 500 (см²)

1 м² = 10 000 см²

10 000 : 2 500 = 4 (шт.) – ламината в 1 м².

56 ∙ 4 = 224 (шт.) – ламината потребуется.

Ответ: 224 штук ламината.

Задача

Для покраски пола комнаты площадью 35 м² купили 3 кг краски. Хватит ли этой краски, если на 1 м² пола расходуется 100 г краски.

Выразим 3 кг в граммах.

1 кг = 1 000 г

3 кг = 3 000 г

35 ∙ 100 = 3 500 (г) – краски потребуется.

3 500 – 3000 = 500 (г) – краски не хватит для покраски пола.

Ответ: 500 г краски не хватит.

Решите аналогичную задачу самостоятельно и проверьте по образцу.

Задача

Стены комнаты решили оклеить обоями. Площадь поверхности составляет 80 м². На одной стене есть окно – 3 м², а на другой – дверь занимает 4 м². Хватит ли 7 рулонов обоев, если в одном рулоне 10 м² обоев.

Проверь себя.

3 + 4 = 7 (м²) – занимают окно и дверь.

80 – 7 = 73 (м²) – нужно оклеить обоями.

7 ∙ 10 = 70 (м²) – в семи рулонах.

73 – 70  = 3 (м²) – обоев не хватит.

Ответ: не хватит 3 м².

Ребята, на уроке мы учились делить на трехзначное число без остатка и с остатком, решали сложные задачи с единицами площади. А теперь настало время подвести итоги! Устроим небольшое соревнование на звание «Знатока математики».

Решите примеры за одну минуту!

(12 543 – 3 890 + 15 498) ∙ 69 ∙ 0 ∙594 =

640 ∙5 ∙0 +640 : 1 – 630 =

? + 150 – 240 – 10 + 26 = 526

Проверь себя.

0, 10, 600.

Кому удалось справиться с заданием за одну минуту, может смело назвать себя большим молодцом!

В первом и втором выражениях самые наблюдательные заметили умножение на нуль (можно не вычислять все выражение, а ∙ 0 = 0).

В третьем выражении первое число можно быстро найти, вычисляя с конца обратным действием: 526 – 26 + 10 + 240 – 150 = 600

Умножение и деление круглых чисел

Обратите внимание: круглым называется число, которое оканчивается нулем — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Круглые числа похожи на десятки

Разряд единиц круглых десятков равняется нулю.

Прочитайте таблицу круглых чисел:

Умножение и деление круглого двухзначного числа на однозначное выполняется по определенным правилам. Познакомьтесь с этими правилами.

Деление круглых чисел

Рассмотрим пример внетабличного деления:

В примерах деления круглого числа делим количество десятков и дописываем в ответе нуль.

Делим на 10 — убираем в ответе нуль.

В частном не пишем нули, если делимое, делитель — круглые числа.

Умножение круглых чисел

А знаете ли вы, что за тысячелетия развития математики было придумано много вариантов умножения. Считалось, что для овладения искусством вычисление нужен талант. Итальянский математик 15 века Лука Пачоли  приводит 8 способов. Познакомимся с некоторыми из них.

Рассмотрите прием внетабличного умножения.

Двадцать умножить на три равно шестидесяти.

Воспользуемся правилом перестановки множителей, получим пример, который умеем решать.

Прочитайте правило внимательно.

При умножении круглого числа на однозначное, надо умножить десятки на второй множитель, в ответ справа добавить нуль.

Увеличить в десять раз — это значит написать в значение произведения первый множитель и добавить к нему 0 справа.

Произведение семи и десяти равно семидесяти.

Воспользуйтесь правилами математики внетабличного умножения и деления для решения примеров:

Проверьте:

Ошибок нет, молодцы. Ваша первая награда — красная ленточка.

Впереди ждут новые открытия, не отставайте, думайте, решайте.

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.

  Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.

• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.

• «Ищем дерево».

  Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.

Этот вариант оставим на крайний случай.

Методика обучения делению в столбик

Чтобы приступить к этому арифметическому действию, нужно познакомить ребенка с названием элементов при делении.

Делимое – число, что подвергается делению, делится на делитель, в результате получается частное.

Объясняют ему саму суть операции деления столбиком. Это такое действие в математике, которое применяют для разделения чисел за счет дробления самого процесса деления на более простые шаги.

Деление в столбик на конкретном примере

Метод деления, основанный на конкретном примере, очень распространен и используется школьниками в дальнейшей учебе. Ребенку предлагается разделить число 945 на 5 в столбик.

Шаг 1. На этом этапе нужно попросить ребенка показать компоненты деления. Если он правильно усвоил выше изложенный материал, то без особых усилий определит: 945 – это делимое, 5 – делитель, результат деления – частное. Собственно, это то, что и необходимо найти.

Шаг 2. Сначала ребенка просят записать рядом 945 и 5, а потом делят их «уголком».

Шаг 3. Следующий этап, просят ребенка рассмотреть делимое и, продвигаясь вправо, предлагают определить самое меньшее число, что больше делителя. Ученик определяет числа: 9, 94 и 945. Самым меньшим из них является 9. Потом спрашивают, сколько раз 5 помещается в числе 9? Ребенок дает ответ, что один раз. Значит, пишут 1 под чертой – первую цифру искомого частного.

Вот и столбик скоро получится.

Шаг 4. На следующем этапе предлагают ребенку умножить 1 на 5 и получают 5. Просят записать результат, который получили, под первой цифрой делимого, и из 9 вычитают 5. Спрашивают ребенка о результате и получают 4.

Здесь важно объяснить ему, что результат вычитания всегда будет меньше делителя. А когда наоборот, значит, неправильно удалось определить, сколько раз 5 содержится в 9. Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого

Ребенок определяет 4 и пишет к четверке

Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого. Ребенок определяет 4 и пишет к четверке.

Шаг 5. Дальше задают ему знакомый вопрос о том, сколько раз 5 помещается в 44? Ученик отвечает, что восемь раз. Тогда предлагают записать восьмерку к единице под чертой. Объясняют ребенку, что это будет следующая цифра искомого частного. Просят умножить 5 на 8. Получается 40, и записывают эту цифру под 44.

Шаг 6. На следующем этапе вся операция повторяется. Ученик вычитает 40 из 44, и получает 4 (4 меньше 5, значит, ребенок все делает правильно). Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.

Шаг 7. Просят его записать девятку под чертой. Предлагают умножить 5 на 9. Ребенок говорит, что получает в результате 45 и записывает в столбик под 45. Дальше проводит вычитание 45 из 45, и получает 0. Ему объясняют, что это был пример деления числа без остатка.

Когда ребенок неплохо умеет пользоваться таблицей умножения, деление в столбик для него простой задачей

Очень важно с помощью постоянных примеров и упражнений закрепить полученный навык

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку»

Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик