Деление двузначных, трехзначных и многозначных чисел столбиком

Пример деления столбиком

Предположим, что нам нужно разделить число 102 на 4

Разберем это на картинке :

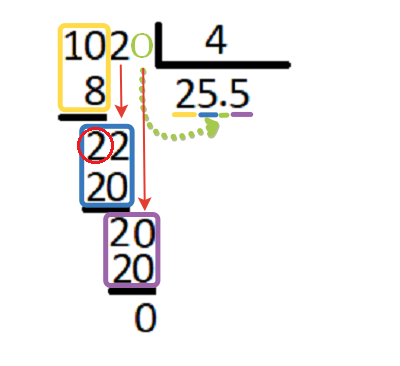
Первое, поскольку у нас цифра 4 однозначное, то проверяем первую цифру слева — это 1, то понятно, что 1 меньше 4, а нам нужно наоборот. Например, если бы перове число слева было бы рано 5, то нам не пришлось бы брать вторую цифру в делимом.

Берем двузначное число слева — это 10 и сравниваем с нажим делителем… 10 больше 4, теперь, все правильно, далее нам потребуется узнать «нод» двух чисел.

Не буду повторять, что такое «нод» — лишь покажу на примере, как мы видим, цифру 10 и делитель 4, то их общий нод будет 2. Или другими словами, в числе 10 умещается всего 2 числа 4…

Этот нод заносим под горизонтальную черту в область частного и умножаем его на 4 — это будет 8, и 8 ставим под ноль

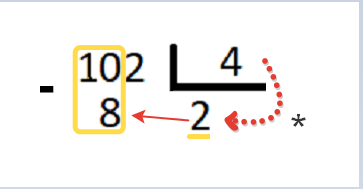
От 10 отняли 8 и ставим его под черту под цифру 8 и если это число получилось меньше 4, то значит нод был найден верно! И нодом нам придется пользоваться много раз, поэтому нужно научиться его находить!

Теперь, у нас в самом верху еще осталась одна двойка, её сносим ниже к двойке, которая получилась отниманием от 10 восьмерки, получается число 22.

Далее опять находим нод чисел 22 и 4 — это 5,

5 заносим его под черту, ставим его после первого найденого нода.

Умножаем 5 на 4 — это будет 20,

20 ставим под 22.

Отнимем опять и получим 2 — это остаток.

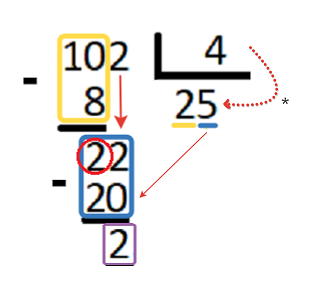
Поскольку у нас наверху не осталось цифр, то ставим 0 и у нас получается 1020 — это означает, что мы перешли из целых в десятые, поэтому, под черту, рядом с пятеркой ставим точку(или запятую(зависит от того, как вас будут учить… )).

Сносим наш ноль до остатка, что получается 20.

Находим нод 20 и 4 — это опять 5.

Заносим 5 под черту рядом с запятой.

Умножаем 4 на 5 = 20.

Ставим его под нашим остатком и нулем.

Отнимаем — получаем ноль.

Правило встречается в следующих упражнениях:

2 класс

Страница 67. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2

3 класс

Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 74,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 11. Вариант 2. № 1,
Моро, Волкова, Проверочные работы

Страница 29. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 40. Вариант 1. № 6,
Моро, Волкова, Проверочные работы

Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 13. Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы

Страница 85. Вариант 2. Тест 3,
Моро, Волкова, Проверочные работы

Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 441,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 673,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 36,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1,
Мерзляк, Полонский, Якир, Учебник

Упражнение 520,
Мерзляк, Полонский, Якир, Учебник

Упражнение 656,
Мерзляк, Полонский, Якир, Учебник

Упражнение 657,
Мерзляк, Полонский, Якир, Учебник

Упражнение 673,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1050,
Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 1211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1222,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1262,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1266,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Пример деления

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

• Напишите в тетради пример: 105 разделить на 5.
• Запишите это, как при делении в столбик.
• Расскажите, что 105 – делимое, а 5 – делитель.
• С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
• В столбике деления, под числом 5, напишите цифру 2.
• Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
• Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
• В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.

Еще один пример деления

Деление столбиком многозначных натуральных чисел

Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел. Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.

На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2, 3 и 4 пункте алгоритма до получения конечного результата.

Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.

Пример.

Выполним деление столбиком многозначных натуральных чисел 5 562 и 206.

Решение.

Так как в записи делителя 206 участвуют 3 знака, то смотрим на первые 3 цифры слева в записи делимого 5 562. Эти цифры соответствуют числу 556. Так как 556 больше, чем делитель 206, то число 556 принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.

Теперь умножаем делитель 206 на числа , 1, 2, 3, … до того момента, пока не получим число, которое либо равно 556, либо больше, чем 556. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0<556, 206·1=206<556, 206·2=412<556, 206·3=618>556. Так как мы получили число, которое больше числа 556, то под выделенным числом записываем число 412 (оно было получено на предпоследнем шаге), а на место частного записываем число 2 (так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:

Выполняем вычитание столбиком. Получаем разность 144, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.

Под горизонтальной линией справа от имеющегося там числа записываем цифру 2, так как она находится в записи делимого 5 562 в этом столбце:

Теперь мы работаем с числом 1 442, выделяем его, и проходим пункты со второго по четвертый еще раз.

Умножаем делитель 206 на , 1, 2, 3, … до получения числа 1 442 или числа, которое больше, чем 1 442. Поехали: 206·0=0<1 442, 206·1=206<1 442, 206·2=412<1 332, 206·3=618<1 442, 206·4=824<1 442, 206·5=1 030<1 442, 206·6=1 236<1 442, 206·7=1 442. Таким образом, под отмеченным числом записываем 1 442, а на месте частного правее уже имеющегося там числа записываем 7:

Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:

Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:

Итак, 5 562:206=27.

Ответ:

5 562:206=27.

Ну и для закрепления материала приведем еще один пример деления столбиком многозначных натуральных чисел.

Пример.

Разделите многозначное натуральное число 238 079 на двузначное натуральное число 34.

Решение.

Удобнее всего деление провести в столбик

Таким образом, неполное частное равно 7 002, и остаток от деления равен 11.

Ответ:

238 079:34=7 002 (ост. 11).

Список литературы.

• Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
• Математика. Любые учебники для 5 классов общеобразовательных учреждений.

Решение задач с единицами площади

Ребята, взрослые люди часто испытывают досаду, занимаясь ремонтом дома или квартиры. Почему? Знакома ситуация, когда чуть-чуть не хватило краски или обоев? Нужно срочно бежать в магазин, чтобы купить недостающие материалы. Можно ли этого избежать? Конечно, можно! Главное, правильно выполнить расчеты. Например, правильно измерить площадь пола под покраску или площадь стен под обои.

Задача

В комнате длиной 7 м и шириной 8 м укладывают на пол ламинат квадратами 50х50 см. Сколько штук ламината потребуется для этой комнаты?

Подсказка. Вычислите площадь комнаты и площадь одного квадрата ламината. Одинаковые ли единицы площади вы использовали? Выразите квадратные метры в квадратных сантиметрах.

Решите задачу самостоятельно.

Проверь себя.

S пола = 7 ∙ 8 = 56 (м²)

S лам. = 50 ∙50 = 2 500 (см²)

1 м² = 10 000 см²

10 000 : 2 500 = 4 (шт.) – ламината в 1 м².

56 ∙ 4 = 224 (шт.) – ламината потребуется.

Ответ: 224 штук ламината.

Задача

Для покраски пола комнаты площадью 35 м² купили 3 кг краски. Хватит ли этой краски, если на 1 м² пола расходуется 100 г краски.

Выразим 3 кг в граммах.

1 кг = 1 000 г

3 кг = 3 000 г

35 ∙ 100 = 3 500 (г) – краски потребуется.

3 500 – 3000 = 500 (г) – краски не хватит для покраски пола.

Ответ: 500 г краски не хватит.

Решите аналогичную задачу самостоятельно и проверьте по образцу.

Задача

Стены комнаты решили оклеить обоями. Площадь поверхности составляет 80 м². На одной стене есть окно – 3 м², а на другой – дверь занимает 4 м². Хватит ли 7 рулонов обоев, если в одном рулоне 10 м² обоев.

Проверь себя.

3 + 4 = 7 (м²) – занимают окно и дверь.

80 – 7 = 73 (м²) – нужно оклеить обоями.

7 ∙ 10 = 70 (м²) – в семи рулонах.

73 – 70  = 3 (м²) – обоев не хватит.

Ответ: не хватит 3 м².

Ребята, на уроке мы учились делить на трехзначное число без остатка и с остатком, решали сложные задачи с единицами площади. А теперь настало время подвести итоги! Устроим небольшое соревнование на звание «Знатока математики».

Решите примеры за одну минуту!

(12 543 – 3 890 + 15 498) ∙ 69 ∙ 0 ∙594 =

640 ∙5 ∙0 +640 : 1 – 630 =

? + 150 – 240 – 10 + 26 = 526

Проверь себя.

0, 10, 600.

Кому удалось справиться с заданием за одну минуту, может смело назвать себя большим молодцом!

В первом и втором выражениях самые наблюдательные заметили умножение на нуль (можно не вычислять все выражение, а ∙ 0 = 0).

В третьем выражении первое число можно быстро найти, вычисляя с конца обратным действием: 526 – 26 + 10 + 240 – 150 = 600

Задачи, которые решаются при помощи действия деления

В курсе математики
средней школы наиболее часто используется деление при решении таких задач,
когда нужно:

• Узнать, во сколько раз одно число меньше и больше другого? Этот вопрос может звучать по-другому: сколько раз меньшее число содержится (помещается) в большем? Или: сколько раз поместится в большем числе меньшее?Например: сколько пятиграммовых стиков сахара находится в килограммовой упаковке? (1000 г : 5 г = 200 шт.).
• Число разделить на заданное количество равных частей.Например: сколько получится грамм сахара в каждом пакете, если пересыпать килограмм сахара в 5 одинаковых пакетов поровну? (1000 г : 5 шт. = 200 г).
• Уменьшить число в заданное количество раз.Например: для приготовления блюда на 5 человек использовали 1 кг сахара, а сколько сахара потребуется для приготовления этого же блюда для одного человека? (1000 г : 5 чел. = 200 г).

Деление суммы на число

Прочитайте рассказ «Из истории символов».

Люди сначала умножали, делить научились позднее. В десятом веке ученый Герберт в математических трудах упомянул сложные правила «железного деления». Старинная итальянская поговорка гласила: «Трудное дело — деление»

Оно и в самом деле было трудно, если принять во внимание утомительные методы, какими выполнялось тогда это действие. 

В середине 18 века в странах Европы начали делить привычным для нас простым способом, который изобрели арабы. Он получил название «золотое деление».

Для записи действия применяются разные знаки:

В 17 веке в Англии и США чаще всего использовался обелюс. Символ в виде двух точек придумал немецкий математик Г. Лейбниц в 1684 году. На письме он очень похож на двоеточие.

Познакомимся со способом деления. Выполните задание.

Какие числа нужно вставить в «окошки», чтобы получились верные равенства?

Решение.

Рассуждаем: первое слагаемое — круглое число. В окошко нужно подставить слагаемое, которое делится на три без остатка.

Подсказка: вспомните результаты табличного умножения на 3. Например, 27.

Деление суммы чисел 30 и 27 на данное число 3 вычисляется так: каждое слагаемое делится на три и результаты складываются.

Запишите подробное решение:

Сформулируйте правило деления суммы на число:

Голубой цвет неба на маршруте вам не помешает.

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.

  Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.

• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.

• «Ищем дерево».

  Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.

Этот вариант оставим на крайний случай.

Правило встречается в следующих упражнениях:

2 класс

Страница 57. Вариант 2. № 3,
Моро, Волкова, Проверочные работы

Страница 66. Вариант 1. Тест 2,
Моро, Волкова, Проверочные работы

Страница 73,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 103,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

3 класс

Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 110,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 59,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 72,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 78,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 13. Вариант 2. Тест,
Моро, Волкова, Проверочные работы

Страница 18. Вариант 1. № 4,
Моро, Волкова, Проверочные работы

Страница 55. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

4 класс

Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 20,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 79,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 50. Вариант 1. Тест 1,
Моро, Волкова, Проверочные работы

Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 102,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 441,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 673,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 36,
Мерзляк, Полонский, Якир, Учебник

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Номер 520,
Мерзляк, Полонский, Якир, Учебник

Номер 656,
Мерзляк, Полонский, Якир, Учебник

Номер 657,
Мерзляк, Полонский, Якир, Учебник

Номер 673,
Мерзляк, Полонский, Якир, Учебник

Номер 1050,
Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 1211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1222,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1262,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1266,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1473,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Деление на 10, 100, 1000 и т.д.

Сразу сформулируем правило деления на натуральных чисел на 10, 100, 1000 и т.д. Сразу будем считать, что деление без остатка возможно.

Деление на 10, 100, 1000 и т.д.

Результатом деления натурального числа на 10, 100, 1000 и т.д. является такое натуральное число, запись которого получается из записи делимого если справа от него отбросить 1, 2, 3 и т.д. нулей.

Отбрасывается столько нулей, сколько из есть в записи делителя!

Например, 30÷10=3. От числа 30 мы отбросили один нуль.

Частное 120000÷1000 равно 120 — от числа 120000 отбрасываем справа три нуля, именно столько их содержится в делителе.

Обоснование правила строится на правиле умножения натурального числа на 10, 100, 1000 и т.д. Приведем пример. Пусть нужно разделить 10200 на 100.

10200=102·100

10200÷100=102·100100=102.

Проверка результата деления чисел делением

Рассмотренный выше способ проверки основан на умножении. Существует также проверка делением. Как ее проводить?

Проверка результата деления

Чтобы проверить верно ли найдено частное, нужно делимое разделить на полученное частное. В результате должен получится делитель.

Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.

Правило основано на той же связи между делимым, делителем и частным, что и правило из предыдущего пункта.

Рассмотрим примеры.

Пример 17. Проверка результата деления натуральных чисел

Верно ли равенство:

104÷13=8.

Разделим делимое на частное:

104÷8=80+24÷8=80÷8+24÷8=10+3=13.

В результате получился делитель, значит, деление выполнено верно.

Пример 18. Проверка результата деления натуральных чисел

Вычислим и проверим: 240÷15=?

Представляя делимое в виде суммы, получаем:

240÷15=150+90÷15=150÷15+90÷15=10+6=16.

Проверяем результат:

240÷16=?

240÷16=160+80÷16=160÷16+80÷16=10+5=15.

Деление выполнено верно.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.