9 тренажеров для изучения таблицы умножения

5+ игр для быстрого запоминания таблицы умножения

Чтобы быстро выучить таблицу умножения, ребенку в возрасте 8-10 лет — а именно столько ему во 2-4 классе, когда в программе появляется умножение — стоит подобрать игру по вкусу. Так процесс пойдет намного эффективнее, чем в случае простой зубрежки.

Вот перечень наиболее распространенных и интересных вариантов игрового обучения:

Карточки

Их можно распечатать самостоятельно, а можно приобрести практически в любом детском магазине — настолько эта игра известна и популярна. Набор включает все комбинации множителей из таблицы умножения с ответами на оборотной стороне.

Чтобы быстро выучить их, играть предлагается следующим образом:

1. Игрок тянет пример
2. В случае правильного ответа карточка отправляется в «отбой»
3. В случае неправильного — возвращается в колоду

Повторять перечисленные шаги следует до тех пор, пока в основной колоде не останется карт. За счет того, что сложные примеры возвращаются в стопку и встречаются снова и снова, они запоминаются лучше и прочнее.

Чтобы выучить всю таблицу умножения максимально быстро, попробуйте устроить игру на время. Ребята, занимающиеся во 2-3 классе, наверняка будут в восторге от такой викторины.

Вам на помощь придут развивающие компьютерные игры

Стихотворные примеры

Разучите с ребенком самые простые рифмующиеся примеры из таблицы умножения: пятью пять, шестью шесть и т.д. А можно сразу взять на вооружение стихотворный разбор всей таблицы — например, книгу Андрея Усачева «Таблица умножения в стихах».

Яркие иллюстрации и интересные короткие стишки превратят зубрежку в увлекательную игру. Чтобы быстро выучить таблицу во 2 или 3 классе, такой способ подойдет как нельзя лучше.

Счет на пальцах

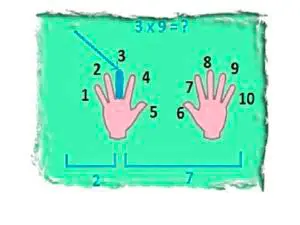
Любознательным детям втянуться в обучение наверняка поможет один наглядный прием-хитрость умножения на девять.

Рассмотрим его на примере пятью девять:

1. Смотрим на собственные ладошки
2. Отсчитываем пятый пальчик слева (как показатель множителя 5)
3. Считаем количество пальцев слева от «множителя» — это десятки (в данном примере их будет четыре)
4. Считаем количество пальчиков справа от пятого — это единицы (в данном примере их пять)

Итогом будет число 45 — ответ на пример из таблицы умножения. Такой подход работает для любых умножений на девять — попробуйте сами.

Ни в коем случае не критикуйте ребенка за неудачи

Использование игрушек или наглядных примеров

Чтобы быстро выучить принципы умножения на 2 и 3 по таблице умножения, можно использовать в качестве подспорья в игре практически что угодно: игрушки, предметы на улице, людей, животных и т.д.

Выберите такой пример, который более знаком и привычен вашему ребенку. Выстраивайте в ряд по два и три игрушки и считайте их. Потом объясните ребенку принцип сокращения процесса подсчета с помощью умножения.

Мобильные или онлайн-игры на изучение таблицы умножения

В сети существует бесчисленное количество разных игр, направленных на то, чтобы быстро выучить таблицу умножения, играя онлайн. Подберите вместе с ребенком увлекательную и яркую игру и предоставьте ему развлекаться — а после проверьте успехи.

Если вас заботит неконтролируемое пребывание ребенка в интернете, выберите игру, которую можно бесплатно скачать, и используйте ее, чтобы быстро выучить таблицу умножения.

Есть много способов привлечь внимание ребенка

Морской бой

Этот игровой способ отлично подходит для закрепления уже имеющихся знаний. Запишите поля «морского боя» цифрами с обеих сторон и установите, что для атаки сектора нужно назвать результат умножения соответствующих чисел.

Такая несложная и увлекательная игра отлично тренирует память и скорость умножения. Конечно, чтобы быстро выучить таблицу умножения во 2 классе, игра нужна не всегда.

Некоторые детки, особенно если им повезло со школьными преподавателями и вообще отношением к учебе, с интересом будут постигать принципы математических примеров и без игр.

В этом случае используйте системный пошаговый подход к обучению:

1. Объясните принцип умножения на единицу и десятку
2. Освойте удвоение
3. Разберите принцип неизменности результата от перестановки множителей
4. Выучите квадраты чисел
5. Последовательно переходите к изучению умножения на 3, 4, 5 и т.д.

Настройтесь на позитивный лад, и результат не заставит себя долго ждать

Даже в такой подход можно добавить игровой элемент, помечая разными цветами уже заученные области. Финальной целью игры будет очищение поля.

Запоминание таблицы умножения — одна из первых ступеней в обучении ребенка математике, одна из важнейших основ. 

Мы уверены, что вы выберете оптимальный подход и успешно изучите все тонкости умножения чисел. Больше наглядного материала по игровому изучению таблицы вы сможете найти в этом видео:

Таблица умножения в стихах

А. Усачев. Таблица умножения в стихах.

Что такое Умножение?
Это умное сложение.
Ведь умней — умножить раз,
Чем слагать всё целый час.

1×1
Один пингвин гулял средь льдин.
Одиножды один — один.

1×2
Один в поле не воин.
Одиножды два двое.

2×2
Два атлета взяли гири.
Это: дважды два — четыре.

2×3
Сел петух до зари
На высокий шест:
— Кукареку!..Дважды три,
Дважды три — шесть!

2×4
В пирог вонзилась пара вилок:
Два на четыре — восемь дырок.

2×5
Двух слонов решили взвесить:
Дважды пять — получим десять.
То есть весит каждый слон
Приблизительно пять тонн.

2×6
Повстречался с раком краб:
Дважды шесть — двенадцать лап.

2×7
Дважды семь мышей —
Четырнадцать ушей!

2×8
Осьминоги шли купаться:
Дважды восемь ног — шестнадцать.

2×9
Вы видали подобное чудо?
Два горба на спине у верблюда.
Стали девять верблюдов считаться:
Дважды девять горбов — восемнадцать.

2×10
Дважды десять — два десятка!
Двадцать, если скажем кратко.

3×3
Кофе пили две букашки
И разбили по три чашки.
Что разбито, то не склеить…
трижды три — выходит девять.

3×4
Целый день твердит в квартире
Говорящий какаду:
— Трри умножить на четырре,
Трри умножить на четырре…
Двенадцать месяцев в году.

3×5
Школьник стал писать в тетрадь:
Сколько будет «трижды пять»?..
Был он страшно аккуратен:
Трижды пять — пятнадцать пятен!

3×6
Стал Фома оладьи есть:
Восемнадцать — трижды шесть.

3×7
Трижды семь — двадцать один:
На носу горячий блин.

3×8
Прогрызли мыши дыры в сыре:
Трижды восемь — двадцать четыре.

3×9
Трижды девять — двадцать семь.
Это нужно помнить всем.

3×10
Три девицы под окном
Наряжались вечерком.
Перстни меряли девицы:
Трижды десять — будет тридцать.

4×4
Четыре милых свинки
плясали без сапог:
Четырежды четыре — шестнадцать голых ног.

4×5
Четыре учёных мартышки
Ногами листали книжки…
На каждой ноге — пять пальцев:
Четырежды пять — двадцать.

4×6
Шла на парад
Картошка-в-мундире:
Четырежды шесть — двадцать четыре!

4×7
Цыплят считают под осень:
Четырежды семь — двадцать восемь!

4×9
У Бабы Яги сломалась ступа:
«Четырежды восемь» — тридцать два зуба! —
Беж жубов ей нечем есть:
— Четырежды девять — «тридцать шешть»!

4×10
Гуляли сорок сорок,
Нашли творожный сырок.
И делят на части творог:
Четырежды десять — сорок.

5×5
Вышли зайцы погулять:
Пятью пять — двадцать пять.

5×6
Забежала в лес лисица:
Пятью шесть — выходит тридцать.

5×7
Пять медведей из берлоги
Шли по лесу без дороги —
За семь верст кисель хлебать:
Пятью семь — тридцать пять!

5×8
Влезть сороконожке
Трудно на пригорок:
Утомились ножки —
Пятью восемь — сорок.

5×9
Встали пушки на пригорок:
Пятью восемь — вышло сорок.

Пушки начали стрелять:
Пятью девять — сорок пять.

5×9
Если лаптем щи хлебать:
Пятью девять — сорок пять…
Будет этот лапоть
Всем на брюки капать!

5×10
Рыли грядку кабачков
Пять десятков пятачков.
И хвостов у поросят:
Пятью десять — пятьдесят!

6×6
Шесть старушек пряли шерсть:
Шестью шесть — тридцать шесть.

6×7
Шесть сетей по шесть ершей —
Это тоже тридцать шесть.
А попалась в сеть плотва:
Шестью семь — сорок два.

6×8
Бегемоты булок просят:
Шестью восемь — сорок восемь…

6×9
Нам не жалко булок.
Рот откройте шире:
Шестью девять будет —
Пятьдесят четыре.

6×10
Шесть гусей ведут гусят:
Шестью десять — шестьдесят.

7×7
Дураков не жнут, не сеют,
Сами нарождаются:
Семью семь — сорок девять…
Пусть не обижаются!

7×8
Раз олень спросил у лося:
— Сколько будет семью восемь? —
Лось не стал в учебник лезть:
— Пятьдесят, конечно, шесть!

7×9
У семи матрёшек
Вся семья внутри:
Семью девять крошек —
Шестьдесят три.

7×10
Учат в школе семь лисят:
Семью десять — семьдесят!

8×8
Пылесосит носом
Слон ковры в квартире:
Восемь на восемь —
Шестьдесят четыре.

8×9
Восемь медведей рубили дрова.
Восемью девять — семьдесят два

8×10
Самый лучший в мире счёт
Наступает Новый год…
В восемь рядов игрушки висят:
Восемью десять — восемьдесят!

9×9
Свинка свинёнка решила проверить:
— Сколько получится «девять на девять»?
— Восемьдесят — хрю — один! —
Так ответил юный свин.

9×10
Невелик кулик, а нос-то:
Девятью десять — девяносто.

10×10
На лугу кротов десяток,
Каждый роет десять грядок.
А на десять десять — сто:
Вся земля как решето!

Другие приемы изучения таблицы умножения

Естественно, единственного верного ответа на вопрос «как правильно учить таблицу умножения» не существует. В каждом отдельном случае, для каждого конкретного ребенка, даже для каждого конкретного урока нужно подбирать определенные наиболее эффективные способы. Попробуйте использовать в своем педагогическом арсенале, несколько приемов работы с вашим ребенком, и тогда вы сможете быстро и легко понять, как лучше научить его таблице умножения. Вот эти способы.

Пример из практики

Выучить любое произведение из таблицы Пифагора будет проще, если продемонстрировать его на практике. Например, у мальчиков можно спросить, сколько всего нужно колес для 5 автомобилей (5×4=20). А таблица умножения для девочек может иметь примеры в стиле, сколько нужно резинок, чтобы заплести по две косички трем куклам (2×3=6).

Сложные примеры

Вашему ребенку какие-то примеры из таблицы умножения могут даваться проще, а какие-то сложнее. Старайтесь тренировать ним именно сложные примеры, чтобы он концентрировался особенно на них.

Таблица умножения на пальцах

Некоторые примеры из таблицы умножения можно легко посчитать, используя пальцы, «природные счеты человека». И это касается не только самых простых произведений, но и, к примеру, умножения на 9. Для этого кладем руки ладонями вниз друг рядом с другом, пальцы нужно выпрямить. Теперь, чтобы умножить любое число на 9 просто загибаем палец под номером этого числа (считая слева). Число пальцев до загнутого будет являться десятками ответа, а после – единицами.

Вообще на пальцах можно считать всю таблицу Пифагора. В данном видео таблицы умножения на пальцах представлены решения более сложных примеров:

Как объяснить принцип работы в таблице умножения

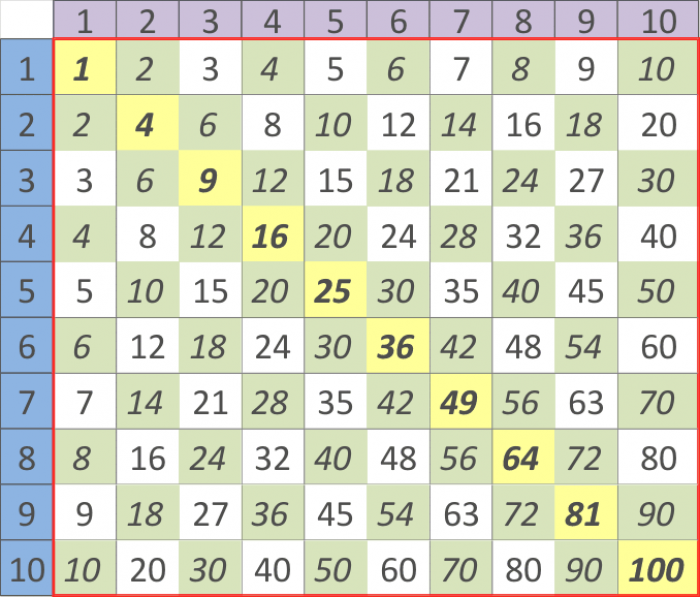
Когда ребёнок изучает таблицу умножения по таблице Пифагора, ему проще увидеть закономерность и симметрию в таблице умножения, и в этом случае он просто запомнит её на всю жизнь, в отличие от простой таблицы, где столбики с примерами. Для ребёнка нужно постараться превратить процесс изучения таблицы умножения в занимательную игру.

После этого нужно начать разбирать процесс устройства таблицы Пифагора. Самое главное в этом процессе показать, что если взять число из левого столбика и умножить его на число из верхней строки, то правильный ответ нужно искать на месте их пересечения. Для этого нужно провести рукой или карандашом по таблице точке пересечения.

Скорее всего, за один раз ребёнок не сможет понять и выучить всё. Для начала нужно начать с колонок 1, 2 и 3, и учить небольшими порциями. Делая так, вы сможете подготовить ребенка к изучению и усвоению таблицы умножения и в другой более сложной информации. После изучения с ребенком азов, можно воспользоваться следующей методикой. Нужно взять пустую нарисованную таблицу Пифагора, и объяснить, как заполнить её самостоятельно. Можно начать с небольшого участка таблица умножения, чтобы ребёнок не запоминал, а учился считать.

Когда ребёнок понял и разобрался, то есть хорошо усвоил самые первые и простые столбцы, правила их умножения, можно перейти  к числам более сложным, сначала к правилу умножения цифр с 4 до 6, и уже после этого умножение чисел от 8 до 10.

На что еще обратить внимание при изучении таблицы умножения с ребенком

Нужно чтобы родители рассказали ребёнку, что такое свойство коммутативности. Это математическое правило о том, что от перестановки множителей произведение не меняется. Если ребёнку правильно и просто объяснить это правило, и показать на конкретных примерах, то ребёнок быстро поймет, что всё не так сложно, и нужно учить на самом деле не всю таблицу умножения, а только её часть. Например, 3 умножить на 7 — это то же самое, что и 7 умножить на 3. То есть, когда он перейдет к изучению крайних столбцов таблицы, умножение чисел в них, он поймёт, что многие примеры по умножению чисел он уже знает. Это очень обрадует ребёнка.

Закономерности в таблице умножения

При изучении таблицы умножения нужно знать и обратить внимание на закономерности в ней, они помогут и упростят запоминание таблицы Пифагора. Рассмотрим некоторые примеры

Если умножить число 1 на любое другое число, то она останется тем же самым. При работе с числом 5 все примеры будут оканчиваться на 5 или на 0. Если число четное, то нужно приписать 0 половине числа, если нечетное, то 5.

Примеры с участием числа 10 заканчиваются на ноль, а начинается с того числа, на которые мы делаем умножение.

Все примеры на 5 меньше чем примеры на 10, например 5 умножить на 10 равно 50, а 5 умножить на 5 равно 2 раза меньше, то есть 25.

При изучении умножении чисел на девять, можно научить ребенка такой закономерности. Нужно записать ответы умножения чисел на 9 в столбик, то есть 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Нужно запомнить самое первое и самое последнее число, То есть 09 и 90. Все остальные числа между ними можно написать и вспомнить по следующему правилу, первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1. То есть, после 09 будет идти число 18, 0 + 1 это 1, а 9 — 1 это 8. И так далее.

Обязательно нужно заниматься с ребёнком, постоянно повторять таблицу умножения. Для начала, когда ребёнок ещё только в процессе изучения, спрашивайте примеры по порядку. Когда же вы заметите, что ребёнок стал отвечать уверенно, то можно спрашивать разброс. Обычно в начале изучения ребенку требуется больше времени на размышления, однако потом можно увеличивать темп и уменьшать время на размышление.

Помогите ребёнку понять физический смысл умножения

Это можно сделать, рисуя на таблице прямоугольники со сторонами, соответствующими умножаемым цифрам.

Например, вот так можно показать, что такое 2 × 4 — это два ряда по четыре клеточки в каждом.

Предложите ребёнку сосчитать, сколько клеточек помещается в получившемся прямоугольнике. Так он сам обнаружит, что 2 × 4 = 8.

Отсканируйте или распечатайте несколько копий таблицы Пифагора и вместе со школьником рисуйте другие прямоугольники — горизонтальные, вертикальные, маленькие и большие, подсчитывая, сколько в них клеточек. Таким образом вы заодно задействуете зрительную память: вспоминая, сколько будет, например, 3 × 4, ребёнок представит себе соответствующую фигуру — и легко ответит.

Иные способы

Чтобы умножение было понятно малышу, нужно объяснить его принцип. Скажем, нам нужно 3 умножить на два. Поясните, что мы берем тройку два раза, а для удобства записываем: 3×2.

Подкрепляем примеры реальными фактами. Задаем жизненный пример. Бабушка принесла два набора карандашей: Васе и Вове. В каждом наборе по 5 карандашей. Сколько всего карандашей получится? Чтобы не складывать, умножаем 5 на 2 и получаем 10.

Лучший способ, как помочь ребятам «справиться» с таблицей Пифагора, — игра. Возьмите кубики и укладывайте их по два в коробку. Посчитайте, сколько пар кубиков получилось. Составьте задачу, скажем, 2×4=8 кубиков. А теперь для наглядности разложите пример и представьте его в виде сложения: 2+2+2+2=2×4=8.

Легче всего выучить наизусть умножение на единицу. Просто объясните ребятам: в результате получается то же число, на которое умножали единицу.

На следующем этапе легче всего запомнить результаты умножения на 2. Нужно просто сложить два одинаковых числа.

Довольно просто научить умножать на 4. Сначала умножить число на 2 (это мы уже умеем), а затем полученный результат еще раз умножить на 2.

При умножении на 5 легко запомнить, что ответ должен заканчиваться на 5 или 0. Это облегчает поиск результата примера.

Самый сложный этап начинается с изучения примеров на 3,6,7 и 8. Приходится подключать другие методики:

Карточки для запоминания. Выберите несколько трудно запоминаемых примеров и напишите их на карточках. Положите их перед ребятами и попросите внимательно посмотреть и запомнить. Затем уберите пособия и попросите малыша восстановить множители и результат. Повторяйте так периодически изо дня в день до тех пор, пока твердо не запомнится материал. В конце обучения можно устроить экзамен. Напишите на отдельных листочках примеры и положите их изображением вниз. Малыш вытягивает пример и говорит ответ на него.

Наглядные пособия. Развесьте таблицу в доме в тех местах, где кроха чаще всего бывает. Пусть она всегда будет на виду

Изредка задавайте малышу примеры, чтобы он обращал внимание на пособия. Стихи

Гуманитариям легче запомнить материал в виде рифмованных четверостиший

Подходящие стихотворения написали М. Казарина и А. Усачев. Мультфильмы. Сегодня существует множество мультиков, в которых герои решают примеры. Одно такой прием хорош только на стадии знакомства.

И еще одна хитрость: объясните, что от перемены мест множителей результат не изменится. Иными словами, 3×4 и 4×3 дают одинаковый ответ: 12.

Перечень описанных приемов решает вопрос, как легко выучить с малышом таблицу Пифагора.

На самом деле вам нужно только знать таблицу на 6

Умножение коммутативно. Если вы знаете 7 x 6 = 42, знайте, что 6 x 7 = 42, если 8 x 6 = 48, то  6 x 8 = 48, и если вы знаете 8 x 7 = 56, вы знаете, что 7 x 8 = 56, и вы будете уметь сократить количество фактов, оставшихся для изучения, до последних шести, упомянутых в начале. Вы можете даже обнаружить, что уже выучили некоторые из этих последних шести, просто прочитав эту статью.

6 х 6 = 36
7 х 6 = 42
8 х 6 = 48
7 х 7 = 49
8 х 7 = 56
8 х 8 = 64

Если вы прочитаете эту статью 2 или 3 раза, вы удивитесь, сколько вы сохраните. Вот и финальная сетка, по-настоящему разделенная и завоеванная!

Я разработал этот метод, когда писал свой блог по математике на GCSE, и мои дети обнаружили, что он им помог. Как вы думаете? Знаете ли вы какие-нибудь другие приемы, которые я должен включить в свой математический блог?

Определение слова «Умножение» по БСЭ:

Умножение — операция образования по двум данным объектам а и b, называемым сомножителями, третьего объекта с, называемого произведением. У. обозначается знаком Х (ввёл англ. математик У. Оутред в 1631) или · (ввёл нем. учёный Г. Лейбниц в 1698). в буквенном обозначении эти знаки опускаются и вместо аЧ b или а · b пишут ab. У. имеет различный конкретный смысл и соответственно различные конкретные определения в зависимости от конкретного вида сомножителей и произведения. У. целых положительных чисел есть, по определению, действие, относящее числам а и b третье число c, равное сумме b слагаемых, каждое из которых равно а, так что ab = а + а +… + а (b слагаемых). Число а называется множимым, b — множителем. У. дробных чисел m &frasl. _n и p &frasl. _q определяется равенством m &frasl. _n · p &frasl. _q = m·p &frasl. _n·q (см. Дробь). У. рациональных чисел даёт число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (-), если они разного знака. У. иррациональных чисел определяется при помощи У. их рациональных приближений.У. комплексных чисел, заданных в форме &alpha. = а + bi и &beta. = с + di, определяется равенством &alpha.&beta. = ac — bd + (ad + bc) i. При У. комплексных чисел, записанных в тригонометрической форме:&alpha. = r₁ (cos&phi.₁ + isin &phi.₁),&beta. = r₂ (cos&phi.₂ + isin &phi.₂),их модули перемножаются, а аргументы складываются:&alpha.&beta. = r₁r₂{cos (&phi.₁ + &phi.₂) + i sin ((&phi.₁ + &phi.₂)}.У. чисел однозначно и обладает следующими свойствами:1) ab = ba (коммутативность, переместительный закон).2) a (bc) = (ab) c (ассоциативность, сочетательный закон).3) a (b + c) = ab + ac (дистрибутивность, распределительный закон). При этом всегда а ·0 = 0. a·1 = а. Указанные свойства лежат в основе обычной техники У. многозначных чисел.Дальнейшее обобщение понятия У. связано с возможностью рассматривать числа как операторы в совокупности векторов на плоскости. Например, комплексному числу r (cos&phi. + i sin &phi.) соответствует оператор растяжения всех векторов в r раз и поворота их на угол&phi. вокруг начала координат. При этом У. комплексных чисел отвечает У. соответствующих операторов, т. е. результатом У. будет оператор, получающийся последовательным применением двух данных операторов. Такое определение У. операторов переносится и на другие виды операторов, которые уже нельзя выразить при помощи чисел (например, линейные преобразования). Это приводит к операциям У. матриц, кватернионов, рассматриваемых как операторы поворота и растяжения в трёхмерном пространстве, ядер интегральных операторов и т.д. При таких обобщениях могут оказаться невыполненными некоторые из перечисленных выше свойств У., чаще всего — свойство коммутативности (некоммутативная алгебра). Изучение общих свойств операции У. входит в задачи общей алгебры, в частности теории групп и колец.

Простые способы обучения детей таблице умножения

Девизом современной педагогики можно считать фразу «обучение с увлечением». Действительно, сегодня и на уроках, и на занятиях дома приветствуется использование игровых методик, интерактивных материалов.

Старый добрый счетный материал, а также разнообразные «подсказки» в виде стишков, песенок и интересных запоминающихся картинок тоже никто не отменял.

Имея представление об основных методиках обучения: запоминание, игра, визуализация – родители в силах самостоятельно научить ребенка таблице умножения.

Запоминание

Задача «выучить таблицу» предполагает в том числе ее буквальное запоминание. Подмечено, что запоминать материал куда легче в стихотворной форме или в виде песенки, особенно если дело касается детей.

Если упорядочить и зарифмовать примеры на умножение, то все нужные числа действительно гораздо быстрее закрепятся в памяти.

Использовать можно любые стихи (к примеру, можно выучить вместе с ребенком слова песни В. Шаинского и М. Пляцковского «Дважды два – четыре»). А родители с фантазией могут подключить ее и придумать свои рифмовки, это легко, например: «шестью семь – сорок два, прилетела к нам сова».

На крайний случай, если таблица уж никак не запоминается, остается рутинный, но проверенный не одним поколением школьников способ – вызубрить ее. Однако имейте в виду, что этот метод детишкам совсем не нравится.

Следует помнить, что запоминание не может быть единственным методом обучения ребенка таблице умножения

Важно не только запомнить последовательность чисел, но и понять суть самого действия. Именно это поможет ребенку в старшем возрасте решать сложные примеры на умножение

Визуализация

Еще одним способом освоения таблицы Пифагора является ее визуализация, предполагающая использование всевозможных наглядных материалов.

Это могут быть:

• счетные материалы;
• картинки;
• и даже пальцы!

С помощью счетного материала, будь то палочки, геометрические фигурки или что-то другое, можно показать ребенку суть умножения («6 х 5» означает «взять 6 раз по 5 предметов»).

Вдобавок, малыш может сосчитать представленные фигурки и убедиться, что ответ получился именно такой, как в таблице Пифагора.

С помощью картинок

Если ребенок любит рисовать – это отличный повод изучить таблицу с помощью картинок.

Принцип действия примерно такой же, как и в случае со счетным материалом, только вместо того, чтоб выложить перед юным математиком 6 раз по 5 палочек можно нарисовать прямо напротив примера 6 квадратов/тортиков/вагонов с 5 точечками/вишенками/зайчиками внутри каждого.

Правда, отрисовывать целые картины при умножении больших чисел будет сложновато.

На пальцах

Хорошим вариантом станет изучение части таблицы Пифагора, а именно столбца с девяткой, на пальцах. Такой своеобразный лайфхак заинтересует любого ребенка.

Расположите кисти рук перед собой ладонями наружу и пронумеруйте их мысленно от 1 до 10, начиная с левого мизинца. Табличные примеры на умножение с числом 9 решаются очень просто: достаточно загнуть палец, номер которого совпадает со вторым множителем.

Так, умножая 3 на 9, загибаем средний палец на левой руке. Пальцы, которые располагаются до загнутого (их два), обозначают количество десятков, а остальные (их семь) – количество единиц.

Итого, в ответе получаем 27. Быстро, легко и интересно!

Посредством обучающих мультфильмов и программ

В качестве средств визуализации, разумеется, можно привлекать обучающие мультфильмы, приложения на мобильных устройствах и программы на ПК, если есть такая возможность и родители не против подобного времяпрепровождения ребенка.

Конечно, для изучения такой непокорной таблицы умножения все средства хороши, но помните, что всего должно быть в меру, и не бросайте малыша на попечение гаджета в этом нелегком деле, а лучше присоединитесь к нему сами.

Игра

Обучение в игровой форме всегда привлекает малышей. Учить таблицу умножения хорошо на материале карточной игры. Из картона делаются карточки на каждый пример таблицы, на одной стороне пишется числовое выражение (5 х 3 = ?), а на другой – ответ.

Игроки по очереди вытягивают карточки, решают пример и проверяют себя, заглянув на обратную сторону. Если ответ правильный, карточка остается у игрока, если нет – возвращается в колоду. Победителем оказывается тот, у кого в конце игры наберется больше всего карточек. 

Таблица Кэли

Таблица Кэли — в общей алгебре, таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Названа в честь английского математика Артура Кэли

Имеет важное значение в дискретной математике, в частности, в теории групп, в которой в качестве операций рассматриваются умножение и сложение. Таблица позволяет определить, является ли группа абелевой, найти центр группы и обратные элементы по отношению к другим элементам в этой группе.

В высшей алгебре таблицы Кэли могут также использоваться для определения бинарных операций в полях, кольцах и других алгебраических структурах. Также они удобны при проведении действий в данных структурах.

Модулярная арифметика

Все остатки от деления на натуральное число образуют кольцо, а от деления на простое число — поле. Это иллюстрируется таблицами умножения:

Таблица умножения в кольце вычетов по модулю 8

×	1	2	3	4	5	6	7
1	1	2	3	4	5	6	7
2	2	4	6	2	4	6
3	3	6	1	4	7	2	5
4	4	4	4	4
5	5	2	7	4	1	6	3
6	6	4	2	6	4	2
7	7	6	5	4	3	2	1

Таблица умножения в поле вычетов по модулю 5

×	1	2	3	4
1	1	2	3	4
2	2	4	1	3
3	3	1	4	2
4	4	3	2	1